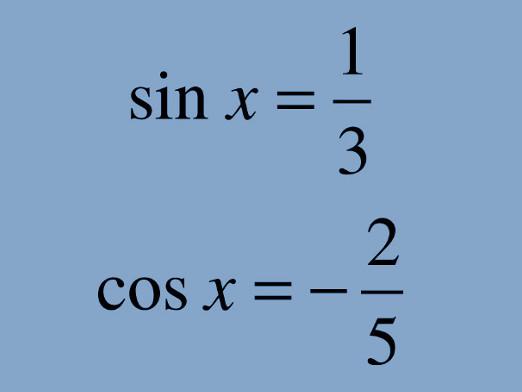วิธีการแก้สมการกำลังสอง

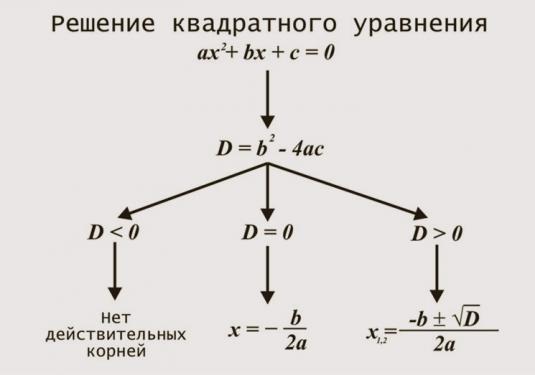
สมการสมการกำลังสองทั้งหมดจะแก้ไขได้โดยการหาตัวจำแนก

จำได้ว่าสมการกำลังสองสมการที่สมบูรณ์คือสมการของแบบฟอร์ม rx²+ wx + h = 0, โดยที่ r, w, h เป็นสัมประสิทธิ์ของสมการกำลังสอง: ตัวเลขบางส่วนไม่เท่ากับศูนย์และ x เป็นตัวแปร (ไม่ทราบ)

วิธีแก้สมการกำลังสองด้วยตัวจำแนก

คำนวณสมการถดถอย (D) ของสมการกำลังสอง คำนวณค่าสัมประสิทธิ์แยกแยะให้หักค่าสัมประสิทธิ์ r และ h โดย 4 จากสัมประสิทธิ์ w w ให้เป็นค่าที่สอง

D = w²- 4rh

ถ้าสมการกำลังสองสมการกำลังสองน้อยกว่าศูนย์ (D <0) สมการนี้ไม่มีรากและไม่มีทางออก

หากมีการแบ่งแยกผลลัพธ์ของตารางสมการเป็นศูนย์ (D = 0) แล้วสมการมีเพียงหนึ่งราก เมื่อต้องการคำนวณรากนี้เราจำเป็นต้องหารสัมประสิทธิ์สมการกำลังสองกับเครื่องหมายลบคูณด้วยค่าสัมประสิทธิ์ r เป็นสองเท่า

นี่คือสูตรสำหรับการค้นหารากเดียว:
x = -w / 2r

ถ้าการแยกแยะผลลัพธ์ของสมการกำลังสองมีค่ามากกว่าศูนย์ (D> 0) รากที่สองจะใช้สมการ

เพื่อค้นหารากแรกของสมการกำลังสอง x₁จำเป็นต้องเพิ่มรากที่สองของตัวจำแนกให้เป็นค่าสัมประสิทธิ์ w ด้วยเครื่องหมายลบและหารผลตามค่าสัมประสิทธิ์ r เป็นสองเท่า

หารากที่สองของสมการ x₂จำเป็นต้องลบรากที่สองของตัวจำแนกออกจากค่าสัมประสิทธิ์ w ด้วยเครื่องหมายลบและหารผลคูณด้วยค่าสัมประสิทธิ์ r

ถ้าสมการกำลังสองสมการที่สมบูรณ์แบบของรูปแบบ rx²+ wx + h = 0 จะลดลงนั่นคือค่าสัมประสิทธิ์ถัดจากที่ไม่รู้จักในสมการที่สองจะเท่ากับความสามัคคี (r = 1) จากนั้นก็สามารถแก้ปัญหาได้ด้วยสูตรของทฤษฎีบทของเวียดนาม

วิธีการแก้สมการกำลังสองลดลงโดยใช้สูตรของทฤษฎีบท Vieta

ทฤษฎีบทของเวียดนามมีดังต่อไปนี้: ผลรวมของรากของสมการกำลังสองลดลงเท่ากับค่าสัมประสิทธิ์ที่สองเท่านั้นที่มีเครื่องหมายตรงกันข้ามและผลคูณของรากเท่ากับระยะฟรี

นั่นคือถ้าสมการของรูปแบบ rx²+ wx + h = 0 มีรากจริงแล้ว

• x₁ + x₂ = -w
• x₁ * x₂ = h

จากสูตรเหล่านี้เราสามารถคาดเดารากของสมการได้ ด้วยเหตุนี้เราจำเป็นต้องขยายระยะฟรี h เป็นสองปัจจัยซึ่งผลคูณจะเท่ากับค่าสัมประสิทธิ์ w ที่มีเครื่องหมายตรงกันข้าม

ตัวอย่างเช่น

เราใช้สมการที่ลดลง x²- 8x + 12 = 0

เรารู้ว่า:

• x₁ + x₂ = 8
• x₁ * x₂ = 12

เราจำเป็นต้องแยกแยะ 12 เป็นสองปัจจัยดังกล่าวซึ่งกันให้ 8 เป็นที่ชัดเจนว่า 6 และ 2 เป็นปัจจัยดังกล่าว

แน่นอน:

• 6 * 2 = 12
• 6 + 2 = 8

เพราะฉะนั้นตัวเลขที่ 6 และ 2 เป็นจริงรากสำหรับสมการกำลังสองลดลง โซลูชั่นที่ชัดเจนดังกล่าวได้อย่างรวดเร็วมาถึงใจเมื่อทำงานกับค่าสัมประสิทธิ์จำนวนเต็มง่ายของสมการกำลังสอง ดังนั้นทฤษฎีบท Vieta มักใช้เพื่อเลือกรากของสมการกำลังสองซึ่งจะช่วยประหยัดเวลาในการแก้ปัญหาเหล่านี้ได้มาก