วิธีการหาพื้นที่ของรูป?

ดูวิดีโอ

รู้และสามารถคำนวณพื้นที่ที่แตกต่างกันได้ตัวเลขมีความจำเป็นไม่เพียง แต่ในการแก้ปัญหาทางเรขาคณิตที่เรียบง่าย อย่าทำโดยปราศจากความรู้นี้และเมื่อร่างหรือตรวจสอบค่าประมาณสำหรับการซ่อมแซมอาคารให้คำนวณจำนวนวัสดุที่จำเป็น ลองหาวิธีหาพื้นที่ที่มีตัวเลขต่างกัน

พื้นที่

ส่วนของเครื่องบินที่ล้อมรอบอยู่ในรูปที่ถูกปิดเรียกว่าพื้นที่ของเครื่องบินลำนี้ พื้นที่แสดงด้วยจำนวนหน่วยที่ล้อมรอบอยู่ในนั้น

เมื่อต้องการคำนวณพื้นที่ของรูปทรงเรขาคณิตพื้นฐานคุณต้องใช้สูตรที่ถูกต้อง

พื้นที่ของรูปสามเหลี่ยม

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
a, b, c คือความยาวของด้านของรูปสามเหลี่ยม,
h คือความสูงของรูปสามเหลี่ยมที่ต้องการ
γคือมุมระหว่างด้าน a และด้าน b,
r คือรัศมีของวงกลม (จารึกไว้ในรูปสามเหลี่ยม),
R คือรัศมีของวงกลม (อธิบายรอบรูปสามเหลี่ยม)
p คือครึ่งหนึ่งของปริมณฑลของรูปสามเหลี่ยม

ถ้า h, a เป็นที่รู้จักแล้วพื้นที่ของรูปสามเหลี่ยมที่ต้องการจะถูกกำหนดให้เป็นผลิตภัณฑ์ของความยาวด้านข้างและความสูงของรูปสามเหลี่ยมลดลงไปทางด้านนี้หารด้วยครึ่ง: S = (a · h) / 2
ถ้ารู้จัก a, b, c เป็นพื้นที่ที่ต้องการคำนวณโดยสูตรของ Heron: รากที่สองนำมาจากผลิตภัณฑ์ครึ่งปริมณฑลของรูปสามเหลี่ยมและสามความแตกต่างของครึ่งปริมณฑลและด้านข้างของรูปสามเหลี่ยมแต่ละอัน: S = √ (p - (p - a) · (p - b) · (p - c))
ถ้า a, b, γเป็นที่รู้จักแล้วพื้นที่ของรูปสามเหลี่ยมถูกกำหนดให้เป็นครึ่งหนึ่งของผลิตภัณฑ์ 2 ด้านคูณด้วยค่ามุมไซนัสระหว่างด้านข้าง: S = (a · b · sin γ) / 2
ถ้า a, b, c, R เป็นที่รู้จักแล้วพื้นที่ที่ต้องการจะถูกกำหนดให้เป็นผลิตภัณฑ์ที่มีความยาวของทุกด้านของรูปสามเหลี่ยมโดยสี่รัศมีของวงกลมที่ล้อมรอบ: S = (a · b · c) / 4R
ถ้า p, r เป็นที่รู้จักแล้วพื้นที่ที่ต้องการของรูปสามเหลี่ยมจะถูกกำหนดโดยการคูณครึ่งปริมณฑลโดยรัศมีของวงกลมที่ถูกจารึกไว้ในนั้น: S = p · r

สี่เหลี่ยมจัตุรัสสี่เหลี่ยม

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
a คือความยาวของด้านข้าง,
d คือความยาวของเส้นทแยงมุม

ถ้าด้านข้างเป็นที่รู้จักแล้วพื้นที่ของรูปนี้ถูกกำหนดให้เป็นรูปสี่เหลี่ยมจัตุรัสยาวด้านข้าง: S = a²
ถ้า d เป็นที่รู้จักกันแล้วสี่เหลี่ยมจัตุรัสจะถูกกำหนดให้เป็นสี่เหลี่ยมครึ่งความยาวของเส้นทแยงมุม: S = d²/ 2

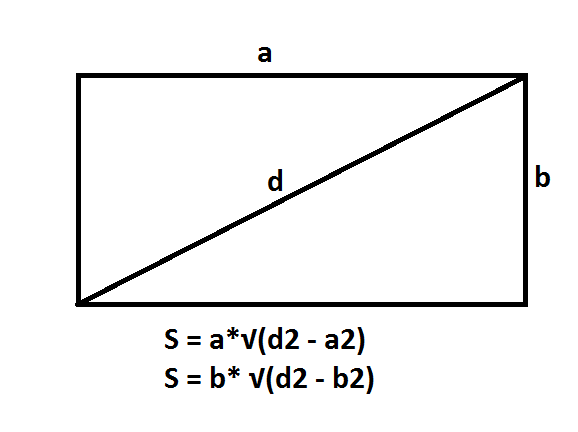
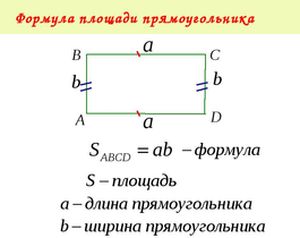
บริเวณสี่เหลี่ยมผืนผ้า

คำอธิบาย:

S คือพื้นที่ที่จะพิจารณา,
a, b คือความยาวของด้านข้างของรูปสี่เหลี่ยมผืนผ้า

ถ้า a, b เป็นที่รู้จักแล้วพื้นที่ของสี่เหลี่ยมผืนผ้านี้จะพิจารณาจากผลคูณของความยาวของสองด้าน: S = a · b
หากความยาวของด้านไม่เป็นที่รู้จักจากนั้นให้แบ่งพื้นที่สี่เหลี่ยมผืนผ้าเป็นรูปสามเหลี่ยม ในกรณีนี้พื้นที่สี่เหลี่ยมผืนผ้ากำหนดเป็นผลรวมของพื้นที่สามเหลี่ยมผืนผ้าที่เป็นส่วนประกอบ

พื้นที่ของรูปสี่เหลี่ยมด้านขนาน

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
a, b คือความยาวของด้าน,
h คือความยาวของความสูงของรูปสี่เหลี่ยมขนมเปียกปูนนี้
d1, d2 เป็นความยาวของสอง diagonals,
αคือมุมระหว่างด้านข้าง,
γคือมุมระหว่างเส้นทแยงมุม

ถ้า a, h เป็นที่รู้จักแล้วพื้นที่ที่ต้องการจะถูกกำหนดโดยการคูณความยาวด้านข้างและความสูงลดลงที่ด้านข้างนี้: S = a · h
ถ้า a, b, αเป็นที่รู้จักแล้วพื้นที่ของรูปสี่เหลี่ยมด้านขนานจะพิจารณาจากการคูณความยาวของด้านของรูปสี่เหลี่ยมด้านขนานและค่าไซน์ของมุมระหว่างด้านข้าง: S = a · b sin sin
ถ้าเรารู้ d₁, d₂, γแล้วพื้นที่ของรูปสี่เหลี่ยมดานเทซ์หมายถึงครึ่งหนึ่งของผลิตภัณฑ์ที่มีความยาวเส้นทแยงมุมและค่าไซน์ของมุมระหว่างเส้นทแยงมุมเหล่านี้: S = (d₁· D₂·Sinγ) / 2

เพชรสแควร์

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
a คือความยาวของด้านข้าง,
h คือความยาวของความสูง,
αเป็นมุมที่เล็กกว่าระหว่างสองด้าน,
d1, d2 เป็นความยาวของเส้นทแยงมุมสองเส้น

ถ้า a, h เป็นที่รู้จักแล้วพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนจะถูกกำหนดโดยการคูณความยาวของด้านข้างโดยความยาวของความสูงที่ลดลงไปด้านนี้: S = a · h
ถ้า a เป็นที่รู้จักกันในนามของαแล้วพื้นที่ที่เป็นรูปสี่เหลี่ยมขนมเปียกปูนจะถูกกำหนดโดยการคูณสี่เหลี่ยมจัตุรัสของความยาวด้านข้างโดยไซน์ของมุมระหว่างด้านต่างๆ S = a²· Sin α
ถ้าเรารู้ d₁ และ d₂จากนั้นพื้นที่ที่กำหนดหมายถึงครึ่งหนึ่งของความยาวของเพชรที่เป็นรูปสี่เหลี่ยมขนมเปียกปูน: S = (d.₁· D₂) / 2

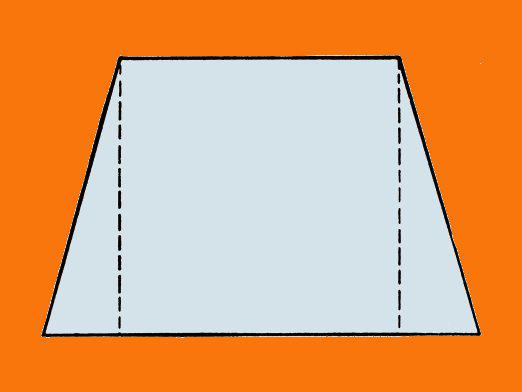
พื้นที่รูปสี่เหลี่ยมคางหมู

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
a, b - ความยาวของฐาน 2 ของ trapezium,
c, d คือความยาวของด้านซ้ายและด้านขวาของ trapezoid,
h คือความสูงของ trapezoid,

ถ้า a, b, c, d เป็นที่รู้จักแล้วพื้นที่ที่กำหนดจะถูกกำหนดโดยสูตร: S = (a + b) / 2 * √ [c²- ((b-a)²+ c²-d²) / (2 (b-a))²]
สำหรับค่า a, b, h, พื้นที่ที่กำหนดหมายถึงผลคูณของครึ่งหนึ่งของฐานและความสูง trapezium: S = (a + b) / 2 · h

พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
d₁, d₂ - ความยาวของเส้นทแยงมุมของรูปสี่เหลี่ยมจัตุรัสที่กำหนด,
αคือมุมระหว่างเส้นทแยงมุม,
p = (a + b + c + d) / 2 คือครึ่งหนึ่งของปริมณฑลของรูปสี่เหลี่ยมนูน,
a และ b, c และ d คือความยาวของแต่ละด้านของรูปสี่เหลี่ยมขนม,
θ = (α + β) / 2 คือครึ่งหนึ่งของผลรวมของสองมุมที่ตรงกันข้ามของจัตุรัสนูน,
r คือรัศมีของวงกลมที่จารึกไว้ในรูปสี่เหลี่ยมขนม

ถ้าเรารู้ d₁, d₂, αแล้วพื้นที่ของรูปสี่เหลี่ยมขนมเป็นนิลเป็นครึ่งหนึ่งของผลิตภัณฑ์ของเส้นทแยงมุมของรูปสี่เหลี่ยมคูณด้วยมุมไซนัสระหว่างเส้นทแยงมุมเหล่านี้: S = (d₁· D ₂· Sin α) / 2
สำหรับรู้จัก p, r พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนถูกกำหนดให้เป็นผลิตภัณฑ์ของ semiperimeter ของรูปสี่เหลี่ยมขนมเปียกปูนโดยรัศมีของวงกลมที่จารึกไว้ในรูปสี่เหลี่ยมขนมเปียกปูนนี้: S = p · r
ถ้า a, b, c, d, θเป็นที่รู้จักแล้วพื้นที่ของนูนรูปสี่เหลี่ยมขนมเปียกปูนหมายถึงรากที่สองของผลิตภัณฑ์ที่แตกต่างกันในช่วงครึ่งปีและความยาวของแต่ละด้านลบด้วยผลิตภัณฑ์ของความยาวของทุกด้านและโคไซน์สแควร์ของครึ่งบวกของสองมุมที่ตรงกันข้าม S² = (p - a) (p - b) (p - c) (p - d) - abcd · cos²((α + β) / 2)

พื้นที่วงกลม

คำอธิบาย:

S คือพื้นที่ที่ต้องการ,
r คือความยาวของรัศมี,
d คือความยาวของเส้นผ่าศูนย์กลาง

ถ้า r เป็นที่รู้จักแล้วพื้นที่ที่ต้องการจะถูกกำหนดให้เป็นผลิตภัณฑ์ของจำนวนπโดยรัศมีในรูปสี่เหลี่ยมจัตุรัส: S = π r²

ถ้า d เป็นที่รู้จักกันแล้วพื้นที่ของวงกลมถูกกำหนดให้เป็นผลิตภัณฑ์ของจำนวนπตามเส้นผ่าศูนย์กลางหารด้วยสี่: S = (π· d²) / 4

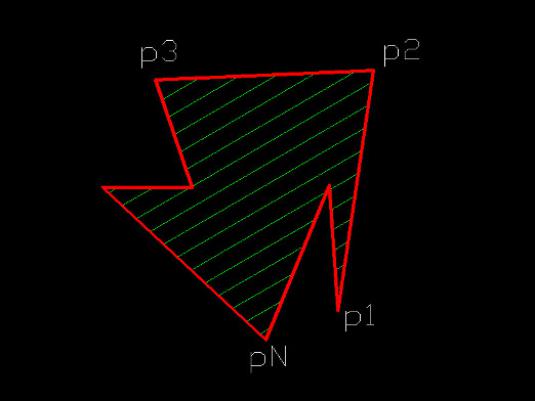
พื้นที่ของรูปที่ซับซ้อน

หนึ่งที่ซับซ้อนสามารถแบ่งออกเป็นรูปทรงเรขาคณิตง่ายๆ พื้นที่ของรูปที่ซับซ้อนหมายถึงผลรวมหรือความแตกต่างของพื้นที่ส่วนประกอบ พิจารณาตัวอย่างเช่นแหวน

แต่งตั้ง:

S คือพื้นที่ของวงแหวน,
R, r เป็นรัศมีของเส้นรอบวงด้านนอกและด้านในตามลำดับ
D, d เป็นเส้นผ่านศูนย์กลางของวงกลมด้านนอกและเส้นรอบวงด้านในตามลำดับ

เพื่อหาพื้นที่ของวงแหวนจึงจำเป็นต้องใช้พื้นที่

วงกลมที่เล็กกว่า S = S1-S2 = π R²-πr²= π (R²-r²)

ดังนั้นถ้า R และ r เป็นที่รู้จักแล้วพื้นที่ของวงแหวนถูกกำหนดให้เป็นความแตกต่างของสี่เหลี่ยมของรัศมีวงกลมด้านนอกและด้านในคูณด้วยจำนวน pi: S = π (R²-r²)

ถ้า D และ d เป็นที่รู้จักแล้วพื้นที่ของวงแหวนถูกกำหนดให้เป็นสี่ส่วนของความแตกต่างของสี่เหลี่ยมขนาดเส้นผ่านศูนย์กลางของวงกลมด้านนอกและด้านในคูณด้วยจำนวน pi: S = (1/4) (D²-d²) π

พื้นที่ของรูปที่แรเงา

สมมติว่ามีอีก (B) (เล็ก) อยู่ในสี่เหลี่ยมเดียวกัน (A) และเราต้องหาช่องที่แรเงาระหว่างตัวเลข "A" กับ "B" สมมติว่า "เฟรม" ของสี่เหลี่ยมเล็ก ๆ เมื่อต้องการทำเช่นนี้: