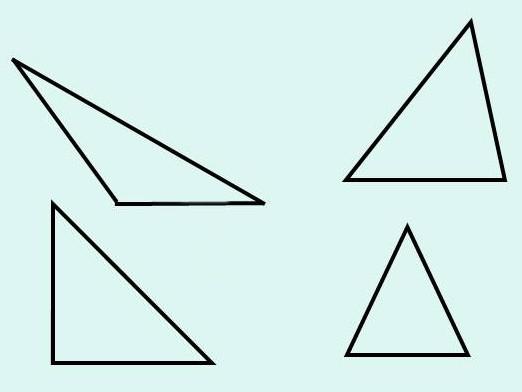
สัญญาณของความเท่าเทียมกันของรูปสามเหลี่ยม

ทุกคนรู้ว่าสองส่วนจะเท่ากันถ้าความยาวของพวกเขาเกิดขึ้น หรือแวดวงสามารถถือได้ว่าเท่ากันหากรัศมีเท่ากัน และสิ่งที่เป็นสัญญาณของความเท่าเทียมกันของสามเหลี่ยม? ชั้นประถมศึกษาปีที่ 7 ของโรงเรียนมัธยมศึกษา: ในบทเรียนเรื่องเรขาคณิตนักเรียนเรียนรู้ว่าจะมีองค์ประกอบที่สามารถพิจารณาความเท่าเทียมกันของรูปสามเหลี่ยมที่มีได้ สะดวกในการใช้แก้ปัญหา

เครื่องหมายแรกของความเท่าเทียมกันของสามเหลี่ยม

การปฏิบัติตามเงื่อนไขของความเท่าเทียมกันสองด้านและมุมที่ล้อมรอบระหว่างพวกเขาในรูปสามเหลี่ยมหนึ่งไปสองด้านและมุมที่ล้อมรอบระหว่างพวกเขาในรูปสามเหลี่ยมอื่นแสดงให้เห็นว่ารูปสามเหลี่ยมดังกล่าวมีค่าเท่ากัน

พิสูจน์

ถ้าเราพิจารณา△ ABC และ△ A1B1C1 โดยที่ด้าน AB = A1B1, BC = B1C1,

และ∠ABCเท่ากับ∠ A1B1C1,

จากนั้น△ A1B1C1 สามารถซ้อนทับบน△ ABC ได้ในลักษณะที่∠ A1B1C1 เกิดขึ้นพร้อมกับ∠ABC ในกรณีนี้รูปสามเหลี่ยมตรงกับที่สมบูรณ์เนื่องจากจุดยอดทั้งหมดของมันตรงกับ

(ถ้าจำเป็นให้ใช้รูปสามเหลี่ยมมุมฉาก A1B1C1 แทน "สามเหลี่ยมสมมาตรเท่ากับ A1B1C1")

เครื่องหมายที่สองของความเท่าเทียมกันของรูปสามเหลี่ยม

หากมีด้านใดด้านหนึ่งและสองมุมที่อยู่ติดกับมันในรูปสามเหลี่ยมตามลำดับมีค่าเท่ากับด้านข้างและสองมุมที่ติดกันในรูปสามเหลี่ยมอื่นแล้วรูปสามเหลี่ยมดังกล่าวถือว่าเท่ากัน

พิสูจน์

ถ้าใน△ ABC และ△ A 1 B 1 C 1 มีความเท่าเทียมกันดังต่อไปนี้

AB = A1B1,

∠BAC = ∠B1A1C1,

∠ABC = ∠A1B1C1

เราวางทับสามเหลี่ยม A1B1C1 และ ABC ไว้ด้วยกันเพื่อให้ด้านเท่ากัน AB และ A1B1 และมุมที่ติดกับพวกเขาตรง. เช่นเดียวกับในตัวอย่างก่อนหน้านี้ถ้าจำเป็นให้ A1B1C1 เป็นรูปสามเหลี่ยมผืนผ้า "หันกลับและวางกลับ" รูปสามเหลี่ยมเรียงกันและดังนั้นจึงสามารถพิจารณาได้ว่าเท่ากัน

เครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยม

หากสามเหลี่ยมของรูปสามเหลี่ยมมีสามเหลี่ยมเท่ากับสามเหลี่ยมในรูปสามเหลี่ยมอื่น ๆ แล้วรูปสามเหลี่ยมดังกล่าวถือว่าเท่ากัน พิสูจน์

สมมติว่าสำหรับ△ ABC และ△ A1B1C1 ความเท่าเทียมกันA1B1 = AB B1C1 = BC C1A1 = CA เลื่อนสามเหลี่ยม A1B1C1 เพื่อให้ด้าน A1B1 สอดคล้องกับด้าน AB และจุด B1 และ B, A1 และ A ตรงตาม เราใช้วงกลมที่มีศูนย์กลาง A และรัศมี AC และวงกลมที่สองมีศูนย์กลาง B และรัศมี BC วงกลมเหล่านี้ตัดกันเป็นสองจุดสมมาตรโดยคำนึงถึงส่วน AB: จุด C และจุด C2 ดังนั้น C1 หลังจากการถ่ายโอนรูปสามเหลี่ยม A1B1C1 ต้องตรงกับจุด C หรือ C2 ในกรณีใด ๆ นี้จะหมายถึงความเท่าเทียม△ ABC = △ A1B1C1 เนื่องจากรูปสามเหลี่ยม△ ABC = △ ABC2 เท่ากัน (อันที่จริงแล้วรูปสามเหลี่ยมเหล่านี้สมมาตรกับส่วน AB)

เครื่องหมายของความสามัคคีของสี่เหลี่ยมผืนผ้า

ในรูปสี่เหลี่ยมผืนผ้ารูปสี่เหลี่ยมผืนผ้ามุมระหว่างขาเป็นเส้นตรงดังนั้นในรูปสามเหลี่ยมรูปสี่เหลี่ยมใด ๆ มีมุมเท่ากันอยู่แล้ว ดังนั้นข้อสังเกตต่อไปนี้ถูกต้อง

• รูปสี่เหลี่ยมผืนผ้ารูปสี่เหลี่ยมผืนผ้ามีค่าเท่ากันถ้าขาของขาข้างหนึ่งมีขนาดเท่ากับขาอื่น ๆ
• รูปสี่เหลี่ยมผืนผ้าสี่เหลี่ยมผืนผ้ามีค่าเท่ากับถ้าเงื่อนไขของความเท่าเทียมกันของด้านตรงข้ามและหนึ่งในขาในรูปสามเหลี่ยมเหล่านี้จะได้พบ

ถ้าเราลบจากเกณฑ์ที่สองซึ่งพูดถึงความเท่าเทียมกันของรูปสามเหลี่ยมเงื่อนไขเกี่ยวกับมุมตรงที่ติดกับขา (เป็นมุมขวาในรูปสามเหลี่ยมเท่ากัน) เรามีดังต่อไปนี้:

• รูปสามเหลี่ยมดังกล่าวมีค่าเท่ากันหากว่า cathetและมุมที่เฉียบพลันติดกับรูปสี่เหลี่ยมผืนผ้าหนึ่งรูปสี่เหลี่ยมผืนผ้าตามลำดับจะมีค่าเท่ากับขาและมุมเฉียบพลันในรูปสามเหลี่ยมสี่เหลี่ยมอีกรูป

เป็นที่ทราบกันดีว่าผลรวมของมุมภายในของรูปสามเหลี่ยมอยู่เสมอ 180 องศาและหนึ่งในมุมของรูปสามเหลี่ยมมุมปากขวาเป็นเส้นตรง ดังนั้นถ้าในรูปสี่เหลี่ยมผืนผ้ารูปสามเหลี่ยมมีมุมที่คมเท่ากันมุมที่เหลือจะเท่ากัน สำหรับรูปสี่เหลี่ยมผืนผ้าธรรมดาสามเหลี่ยมผืนผ้าไม่ใช่รูปสี่เหลี่ยมผืนผ้าในการกำหนดความเท่าเทียมกันของตัวเลขก็จะเพียงพอที่จะรู้ได้ว่าด้านใดด้านหนึ่งและสองมุมที่เท่ากันมีเท่ากันตามลำดับ ในรูปสามเหลี่ยมมุมฉากด้านขวาจะมีเพียงมุมที่เฉียบพลันและด้านตรงข้ามเท่านั้นที่สามารถกำหนดความเท่าเทียมกันของตัวเลขได้

• รูปสี่เหลี่ยมผืนผ้ารูปสี่เหลี่ยมผืนผ้าจะเท่ากันภายใต้เงื่อนไขว่ามุมเฉียบพลันและด้านตรงข้ามของมุมหนึ่งข้างในมุมฉากและมุมฉากตรงข้ามกันมาก

วิทยาศาสตร์มหัศจรรย์ - เรขาคณิต! เครื่องหมายของความเท่าเทียมกันของรูปสามเหลี่ยมจะมีประโยชน์ไม่เพียง แต่สำหรับตำราเรียน แต่ยังสำหรับการแก้ปัญหาในชีวิตประจำวันที่ผู้ใหญ่แก้ปัญหาในชีวิตประจำวัน