วิธีการหามุมเฉียบพลันของรูปสี่เหลี่ยมถูกรูปหรือไม่?

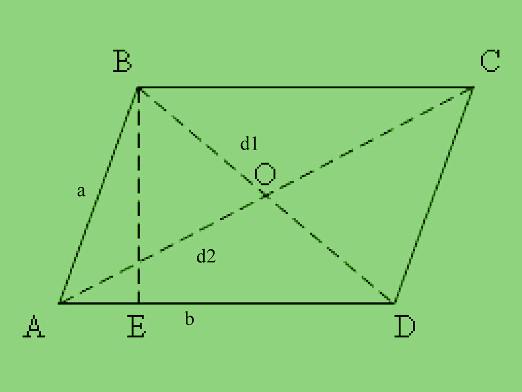
รูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนซึ่งด้านตรงข้ามเป็นคู่ขนาน

รูปสี่เหลี่ยมด้านขนานมีคุณสมบัติทั้งหมดของสี่เหลี่ยมจัตุรัส แต่ก็มีลักษณะเด่นของตัวเอง รู้ว่าเราสามารถหาทั้งสองด้านและมุมของรูปสี่เหลี่ยมขนมเปียกปูน

คุณสมบัติ Parallelogram

ผลรวมของมุมในรูปสี่เหลี่ยมด้านขนานใด ๆ เช่นเดียวกับรูปสี่เหลี่ยมขนมเปียกปูนใด ๆ คือ 360 องศา
เส้นกลางของรูปสี่เหลี่ยมด้านขนานและเส้นทแยงมุมของมันตัดกับจุดหนึ่งและแบ่งเป็นครึ่งหนึ่ง จุดนี้มักเรียกว่าศูนย์กลางของความสมมาตรของรูปสี่เหลี่ยมขนมเปียกปูน
ด้านข้างของรูปสี่เหลี่ยมด้านขนานมีความเสมอภาคเสมอ
นอกจากนี้ตัวเลขนี้ยังมีมุมตรงกันข้าม
ผลรวมของมุมที่อยู่ติดกับด้านข้างของรูปสี่เหลี่ยมด้านขนานอยู่เสมอ 180 °
ผลรวมของสี่เหลี่ยมของเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนานเท่ากับสองเท่าของสี่เหลี่ยมของสองด้านที่อยู่ติดกัน นี่แสดงด้วยสูตร:
- d₁² + d₂²= 2 (a²+ b²) โดยที่ d₁ และ d₂ - diagonals, a และ b - ด้านที่อยู่ติดกัน
โคไซน์ของมุมเอียงมักจะน้อยกว่าศูนย์

วิธีหามุมของรูปสี่เหลี่ยมขนมเปียกปูนการใช้คุณสมบัติเหล่านี้ในทางปฏิบัติ? และสิ่งที่สูตรอื่น ๆ สามารถช่วยเราในเรื่องนี้ได้อย่างไร ลองพิจารณางานเฉพาะที่ต้องการ: หามุมของรูปสี่เหลี่ยม

การหามุมของรูปสี่เหลี่ยมด้านขนาน

กรณีที่ 1. การวัดมุมของมุมเอียงเป็นที่ทราบกันแล้วจำเป็นต้องหามุมเฉียบพลัน

ตัวอย่าง: ในรูปสี่เหลี่ยมด้านขนาน ABCD มุม A คือ 120 ° ค้นหาการวัดมุมอื่น ๆ

วิธีการแก้ปัญหา: การใช้คุณสมบัติเลขที่ 5 เราสามารถหาค่ามุมของมุม B ที่อยู่ติดกับมุมที่ระบุในปัญหา จะเท่ากับ: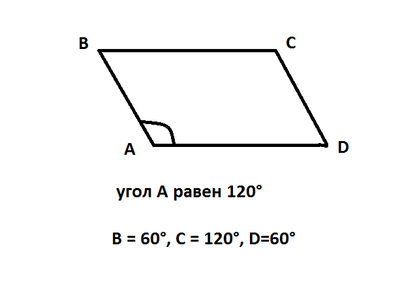

180 ° -120 ° = 60 °

และตอนนี้โดยใช้ทรัพย์สินหมายเลข 4,ว่าทั้งสองมุมที่เหลือ C และ D อยู่ตรงข้ามกับที่เราได้พบแล้ว มุม C อยู่ตรงข้ามกับมุม A มุม D ไปยังมุม B ดังนั้นจะเป็นคู่เท่ากับพวกมัน

คำตอบ: B = 60 °, C = 120 °, D = 60 °

กรณีที่ 2 ด้านและเส้นทแยงมุมเป็นที่รู้จัก

ในกรณีนี้เราต้องใช้ทฤษฎีโคไซน์

แรกเราสามารถคำนวณโคไซน์ของมุมที่เราต้องการจากสูตรแล้วหาจากตารางพิเศษว่ามุมของตัวเองเท่ากับเท่าไร

สำหรับมุมเฉียบพลันสูตรคือ:

cosa = (²² - 2 ²) / (2 * А * ²) ที่
a คือมุมที่ต้องการเฉียบพลัน
A และ B เป็นด้านของรูปสี่เหลี่ยมขนมเปียกปูน,
d - เส้นทแยงมุมเล็ก

สำหรับมุมเอียงสูตรมีการเปลี่ยนแปลงเล็กน้อย:

cosß = (А² + ² - D ²) / (2 * А * ²) โดยที่
ßคือมุมซ้อน,
A และ B เป็นด้าน,
D - เส้นทแยงมุมใหญ่

ตัวอย่าง: จำเป็นต้องหามุมที่เป็นรูปสี่เหลี่ยมด้านขนานที่ด้านข้าง 6 ซม. และ 3 ซม. และเส้นทแยงมุมเล็ก 5.2 ซม.

แทนค่าในสูตรเพื่อหามุมเฉียบพลัน:

cosa = (6² + 3² - 5.2²) / (2 * 6 * 3) = (36 + 9 - 27.04) / (2 * 18) = 17.96 / 36 ~ 18/36 ~ 1/2
cosa = 1/2 จากตารางพบว่ามุมที่ต้องการคือ 60 °
คำตอบ: 60 °

อ่านเพิ่มเติม: