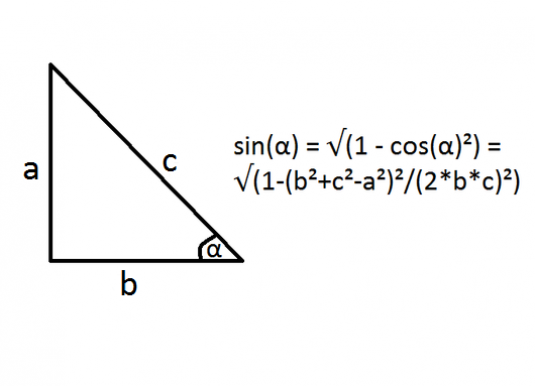วิธีการหาไซน์ของมุมด้านนอก?

มุม Sine ต้องคำนวณไม่ได้เฉพาะในรูปสามเหลี่ยมมุมเขียวเท่านั้น แต่ในรูปอื่น เมื่อต้องการทำเช่นนี้จำเป็นต้องวาดความสูงของรูปสามเหลี่ยม (ตั้งฉากกับด้านใดด้านหนึ่งซึ่งลดลงจากมุมด้านตรงข้าม) และแก้ปัญหาให้เป็นรูปสามเหลี่ยมขนมขอมด้านขวาโดยใช้ขาข้างหนึ่งเป็นเส้นความสูง

วิธีการหาไซน์ของมุมด้านนอกของรูปสามเหลี่ยม

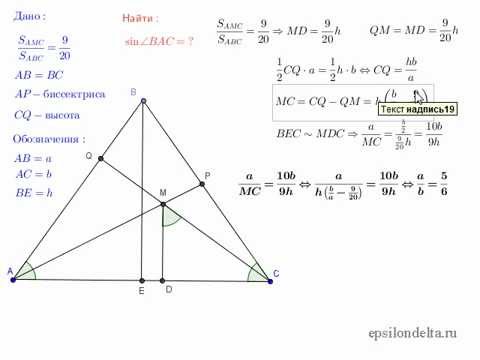
ก่อนอื่นคุณต้องเข้าใจว่ามุมด้านนอกคืออะไร เรามีรูปสามเหลี่ยม ABC โดยพลการ ถ้าด้านใดด้านหนึ่งเช่น AC อยู่เหนือมุม BAC และดึงคาน AO มุม OAB ใหม่จะอยู่ภายนอก ที่นี่เราจะมองหาไซน์ของเขา

เพื่อแก้ปัญหาเราต้องวางแนวตั้งฉาก BH ไปทางด้านข้างของ AU จากมุมเอบีซี นี่คือความสูงของรูปสามเหลี่ยม ขั้นตอนของการแก้ปัญหาจะขึ้นอยู่กับสิ่งที่เรารู้

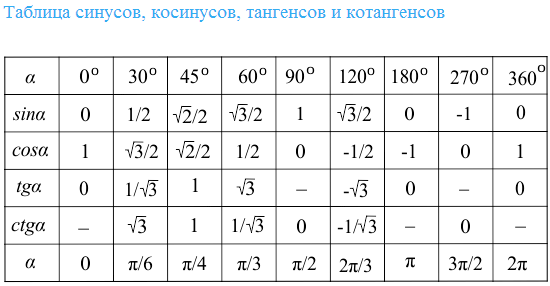
ตัวเลือกที่ง่ายที่สุดคือถ้าคุณรู้มุมของคุณ แล้วปัญหาจะแก้ไขได้ง่ายมาก เนื่องจากรังสีเรย์ OC เป็นเส้นตรงมุม OAC = 180 ° ดังนั้นมุม OAB และ BAC อยู่ติดกันและ Sines ของมุมที่อยู่ติดกันมีขนาดเท่ากัน

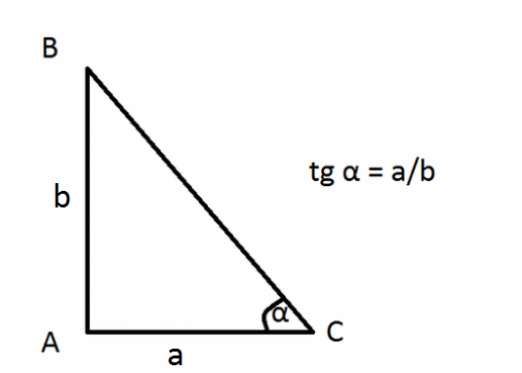
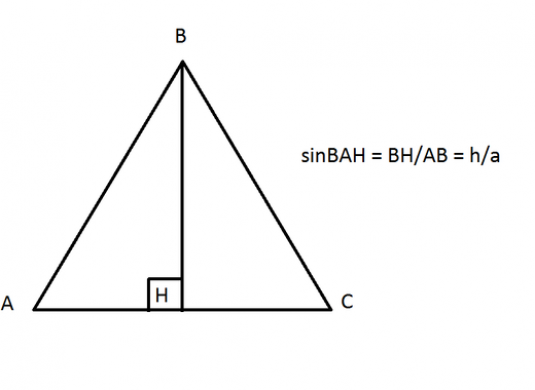
ให้เราพิจารณาปัญหาอื่น: ในรูปสามเหลี่ยม ABC โดยทางด้านข้าง AB = a และความสูง BH = h จำเป็นต้องหาไซน์ของ OAS มุม เนื่องจากตอนนี้เรามีรูปสี่เหลี่ยมผืนผ้า ABN แล้วไซน์ของ ABN จะเท่ากับอัตราส่วนของขา HH กับด้านตรงข้ามของ AB:

• sinBAH = BH / AB = h / a

นี่เป็นเรื่องง่าย ปัญหาที่ซับซ้อนมากขึ้นถ้าความสูง h เป็นที่รู้จักกันและด้าน AC = c, BC = b, มันเป็นสิ่งจำเป็นในการหาไซน์ของมุม OAB

โดยทฤษฎีบทของพีทาโกรัสเราจะพบ catheter ของ CH ของรูปสามเหลี่ยม VSN:

• BC² = BH² + CH²b² = h² + CH ²,
• CH² = b² - h², CH = √ (b² - h²).

จากที่นี่คุณสามารถหาส่วนของด้าน AS ของ AC:

• AH = AC - CH = c - √ (b² - h²)

ตอนนี้เราใช้ทฤษฎีบท Pythagorean เพื่อหาด้านที่สามของรูปสามเหลี่ยม ABN ABN:

• AB² = BH² + AH² = h² + (c - √ (b² - h²)) ²

ไซน์ของมุม BAC เท่ากับอัตราส่วนของความสูงของ HV ของรูปสามเหลี่ยมไปยังด้าน AB:

• sinBAC = BH / AH = h / (c - √ (b² - h²)).

เนื่องจากมุม OAB และ BAC อยู่ติดกัน Sines ของพวกเขามีขนาดเท่ากัน

ดังนั้นการรวมทฤษฎีบทพีทาโกรัสความหมายไซน์และทฤษฎีบทอื่น ๆ (โดยเฉพาะในมุมที่อยู่ติดกัน) ก็เป็นไปได้ที่จะแก้ปัญหาส่วนใหญ่ของปัญหาเกี่ยวกับรูปสามเหลี่ยมซึ่งรวมถึงการหาไซน์ของมุมภายนอก บางครั้งอาจมีการก่อสร้างเพิ่มเติม: วาดความสูงจากมุมที่ต้องการเพื่อดำเนินการต่อด้านข้างของมุมเกินขีด จำกัด และอื่น ๆ