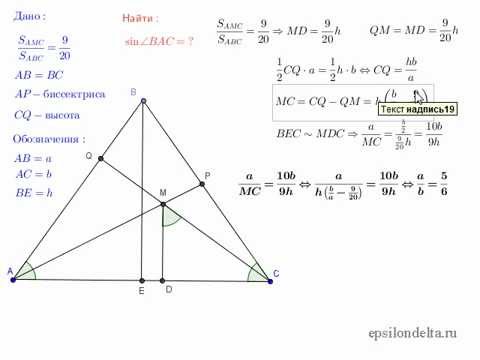
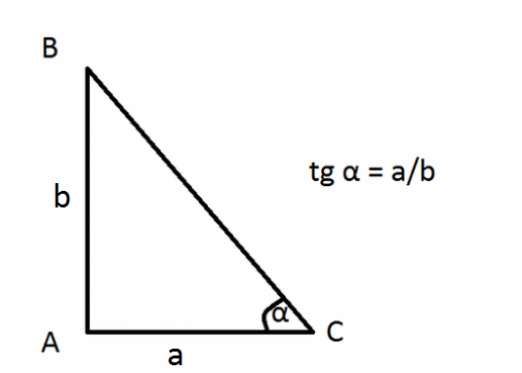
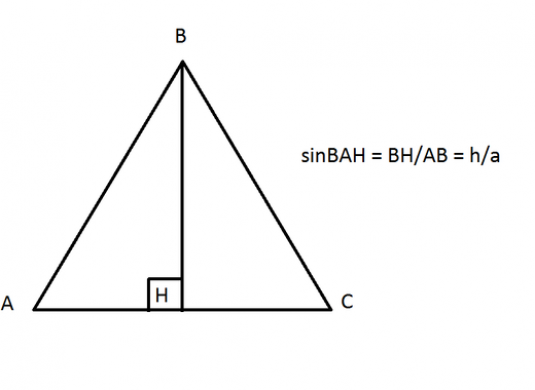
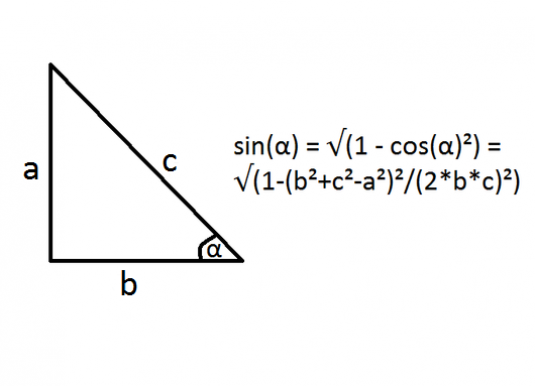วิธีการหาไซน์ของมุมของรูปสามเหลี่ยม?

เพื่อหาไซน์ของมุมของสี่เหลี่ยมรูปสามเหลี่ยมเราต้องจำสิ่งที่เป็นไซน์ตามคำจำกัดความ และความหมายง่ายมาก: ไซน์ของมุมเท่ากับอัตราส่วนของขาตรงข้ามกับด้านตรงข้าม

วิธีการคำนวณ Sines

ถ้าเรามีรูปสามเหลี่ยม ABC ซึ่ง A -มุมขวาแล้วด้าน AB และ AC จะเป็นขาและด้าน BC - ด้านตรงข้าม ดังนั้นโดยความหมายไซน์ของมุม B เท่ากับที่เกี่ยวกับด้านตรงข้ามมุมฉาก AU ขา: sinB = AC / BC ไซน์และมุมอื่น ๆ sinc = AB / BC

ในรูปสามเหลี่ยมมุมฉากด้านขวามีหน้าที่ของมุมมันสะดวกในการคำนวณ: ไม่มีการก่อสร้างเพิ่มเติมเป็นสิ่งจำเป็น ก็พอจะทราบความยาวของด้านขวา แต่บ่อยครั้งเพียงส่วนหนึ่งของข้อมูลที่จำเป็นเป็นที่รู้จักกันส่วนที่เหลือควรจะขอ พิจารณาวิธีการทำเช่นนี้

กำลังมองหาไซน์ด้วยขาสองข้าง

เราใช้รูปสามเหลี่ยม ABC เดียวกันกับมุมฉาก A ซึ่งเราทราบขนาดของขา: AB = a, AC = c ในการคำนวณไซน์ของมุม C นั้นจำเป็นต้องแบ่ง cathete ออกเป็นด้านตรงข้าม:

• sinC = AB / BC = a / BC (1)

แต่ทแยงมุมจะต้องได้รับการพิจารณาตามทฤษฎีบทพีทาโกรัส:

• BC = √ (AB² + AC²) = √ (a² + b²) (2)

เราหาค่าที่พบจากด้านตรงข้าม (2) ใน expression (1) เราได้คำตอบ:

• sinC = a / √ (a² + b²).

กำลังมองหาไซน์ที่ด้านตรงข้ามและขาข้างเคียง

ตอนนี้ในรูปสามเหลี่ยมเดียวกันเราต้องหาไซน์ของมุมเดียวกัน C แต่เราทราบว่าด้านตรงข้ามกัน BC = b และแคโทด AC = c ด้วยความช่วยเหลือของทฤษฎีบทพีทาโกรัส: AB² + AC² = BC²เรามองหา AB:

• AB = √ (b²-c²)

ตอนนี้แทนค่าที่พบจาก AB ในสูตรสำหรับไซน์:

• sinC = AB / b = √ (b²-c²) / b

การคำนวณไซน์ที่ด้านใดด้านหนึ่งและมุมที่คมชัด

ในรูปสามเหลี่ยม ABC มีมุมฉาก A มุม B = βเป็นที่รู้จักและ catethesis AC = c เราต้องหาไซน์ของมุม C.

วิธีที่ 1

ที่ง่ายที่สุด - ถ้าคุณจำได้ว่าผลรวมของทุกมุมในรูปสามเหลี่ยมคือ 180 °:

• A + B + C = 180 °
• มุม A = 90 °, B = β,
• C = 180 ° -90 ° - β = 90 ° - β
• ดังนั้น sinC = sin (90 ° - β).

วิธีที่ 2

แต่คุณสามารถไปในทางอื่น:

• Sinβ = AC / BC; Sinβ = c / BC จากที่นี่:
• BC = c / Sinβ

จากทฤษฎีบทของ Pythagoras AB2 + AC2 = BC2 เราหาด้านตรงข้าม:

• AB = √ (BC²-AC²)

เราแทนค่าที่รู้จัก:

• AB = √ (с² / Sin²β-c²) = √² (1 / Sin²β-1) = с√ (1 / Sin²β-1)

ดังนั้นเราจึงพบไซน์ของมุม C:

• sinC = AB / BC = c√ (1 / Sin²β-1) / s / Sinβ = Sinβ√ (1 / Sin²β-1)

ตอบ:

• sinC = Sinβ√ (1 / Sin²β-1).