วิธีการหาเส้นตรงกลางของหน้าจั่วสี่เหลี่ยมคางหมู?

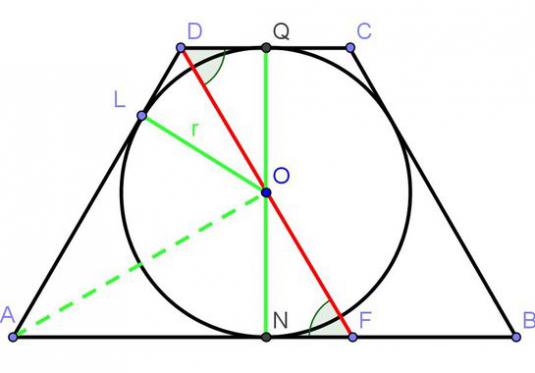
ปกติเรียก trapezium เป็นรูปสี่เหลี่ยมขนมเปียกปูนซึ่งมีเพียงสองด้านขนานกับกันและกัน ด้านข้างเหล่านี้เป็นฐานของ trapezium อีกสองด้านเรียกว่าด้านข้าง

รูปทรงสี่เหลี่ยมคางหมูเรียกว่าหน้าจั่ว (aesceles) ซึ่งความยาวของด้านข้างมีค่าเท่ากัน

เส้นตรง trapezium

เส้นตรงเป็นเส้นที่เชื่อมต่อตรงกลางของทั้งสองด้านของรูป

วิธีการหาเส้นตรงสี่เหลี่ยมคางหมูถ้าเป็นรูปสี่เหลี่ยมคางหมูเป็นหน้าจั่ว?

มีอยู่หลายวิธี

วิธีการหาเส้นกึ่งกลางของหน้าจั่วสี่เหลี่ยมจัตุรัส

วิธีที่ 1

ถ้าเราทราบความยาวของฐานของรูปสี่เหลี่ยมคางหมูแล้วเราจะใช้สูตร:

• m = (a + b) / 2 โดยที่:
• m คือความยาวของเส้นกึ่งกลาง
• a และ b คือความยาวฐาน

วิธีที่ 2

ถ้าเราทราบความยาวของด้านแล้วเราต้องการข้อมูลเพิ่มเติม อาจมีสองกรณี:

กรณี A

เราจะมีความยาวด้านข้างเพียงพอและปริมณฑลของ trapezium

• สูตร: m = (P - 2 * c) / 2, ที่
• m คือเส้นตรง,
• P - ปริมณฑล
• s คือด้านข้าง

กรณีข

นอกจากความยาวของด้านข้างแล้วจำเป็นต้องทราบความยาวของความสูงของรูปสี่เหลี่ยมคางหมูและความยาวของฐาน

สูตร:

• m = a คือรากของ (c² - h²)

หรือ

• m = b + รากของ (c² - h²) ที่
• m - บรรทัดกลาง
• a เป็นพื้นฐานที่มากขึ้น,
• b - ฐานที่เล็กกว่า
• s - side
• h - ความสูง trapezium

ตัวอย่าง

ลองพิจารณาแต่ละกรณีในตัวอย่างที่เฉพาะเจาะจง งานจะเหมือนกันทุกหนทุกแห่ง: หาเส้นตรงกลางของหน้าจั่วสี่เหลี่ยมจัตุรัส

1 วิธี

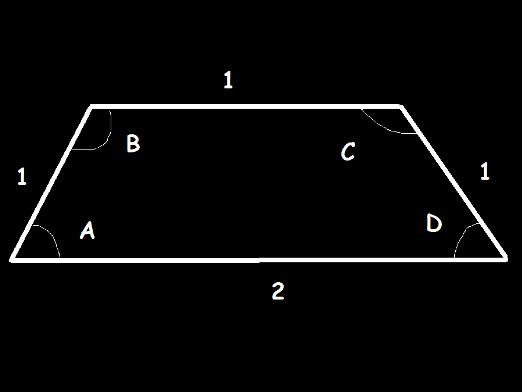
ระบุ: ฐานสี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมคางหมูเป็น 4 ซม. ส่วนที่สองคือ 6 ซม

• วิธีแก้คือ m = (4 + 6) / 2 = 10/2 = 5
• คำตอบ: 5 ซม.

2 วิธีกรณี A

ระบุ: ด้านข้างของหน้าจั่วสี่เหลี่ยมจัตุรัสเป็น 3 ซม., ปริมณฑลคือ 20 ซม.

• วิธีแก้คือ m = (20 - 3 * 2) / 2 = (20 - 6) / 2 = 7
• คำตอบ: 7 ซม

2 วิธีกรณี B

ระบุ: ฐานสี่เหลี่ยมขนาดเล็กของสี่เหลี่ยมคางหมูเป็นสี่เหลี่ยมความสูงของรูปสี่เหลี่ยมคางหมูเป็น 3 ซม. และด้านข้างเป็น 5 ซม.

วิธีการแก้ปัญหา:

เนื่องจากพื้นดินมีให้กับเราน้อยเราจึงเลือกสูตรที่มีเครื่องหมาย +

• m = 4 + รากของ (5²-3²) = 4 + รากของ 16 = 4 + 4 = 8
• คำตอบ: 8 ซม

หากมีขนาดใหญ่ขึ้นตัวอย่างเช่น 13 ซม. ก็ได้การแก้ปัญหาจะมีลักษณะดังนี้:

• m = 13 - รากของ 16 = 13-4 = 9
• คำตอบ: 9 ซม