วิธีคำนวณลูกบาศก์?

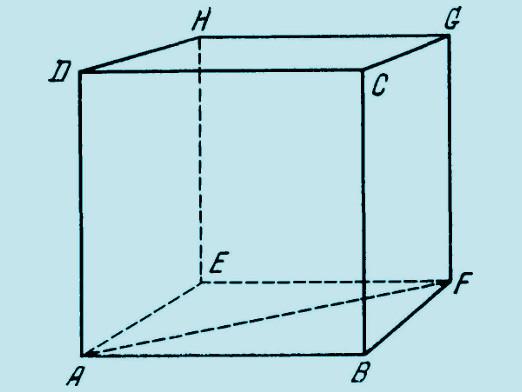
ประการแรกเพื่อทำความเข้าใจเกี่ยวกับการคำนวณพื้นที่ก้อนที่คุณต้องรู้สิ่งที่เป็นตัวเลขนี้ซึ่งมีคุณสมบัติเฉพาะ หลังจากที่ทุกคนทราบว่าเป็นก้อนและที่มีส่วนประกอบหลักที่มันจะง่ายขึ้นในการคำนวณรูปทรงเรขาคณิต ดังนั้นก้อน - เป็นรูปทรงหลายเหลี่ยมปกติแต่ละใบหน้าของตาราง ใบหน้าของลูกบาศก์มีหก นอกจากนี้กรณีที่ก้อนส่วนตัว: ปริซึมและรูปร่างหรือ polyhedrons parallelepiped ข้อมูลที่มีส่วนประกอบอื่น ๆ เช่นปริซึมรวมใบหน้าของพวกเขารูปหลายเหลี่ยมเท่ากันสี่เหลี่ยมด้านขนานและสำหรับกล่อง - ที่นี่สี่เหลี่ยมด้านขนานที่ชัดเจน ก่อนที่คุณจะคำนวณลูกบาศก์เราจะเข้าใจคุณสมบัติของ:

1. ส่วนข้ามของลูกบาศก์เป็นรูปหกเหลี่ยม
2. เส้นทแยงมุมของลูกบาศก์เป็นส่วนที่เชื่อมต่อสองจุดและพวกเขาจะหันสมมาตรไปยังศูนย์กลางของลูกบาศก์
3. เราให้สูตรหลักสำหรับการแก้รูปนี้:

• พื้นที่ของลูกบาศก์ - 6a² ;
• ระดับเสียงคือ - a³ ;
• รัศมีของทรงกลมที่ถูกจารึกไว้ในลูกบาศก์คือ 1/2 * a;
• รัศมีของทรงกลมที่อธิบายไว้คือรากที่มี 3 หารด้วย 2 และคูณด้วย "a"

คำแนะนำสำหรับการคำนวณลูกบาศก์

เนื่องจากคำถามมีความสำคัญกับเรา: วิธีคำนวณลูกบาศก์ลองดูคำแนะนำแบบทีละขั้นตอนในการคำนวณรูปทรงเรขาคณิตนี้:

1. หลังจากที่เราได้ทราบว่ามีอะไรบ้างลูกบาศก์สิ่งที่มีคุณสมบัติสูตรสำหรับการคำนวณส่วนประกอบหลักของมันมีความจำเป็นต้องยอมรับการคำนวณ ประการแรกต้องใส่ใจกับข้อมูลที่คุณมีอยู่ (ขนาดของด้านยาวของเส้นทแยงมุม) ถ้าไม่มีข้อมูลใด ๆ คุณควรทำอย่างเรียบง่าย - ตั้งชื่อขอบลูกบาศก์ "a" เพิ่มเติมในการคำนวณเริ่มต้นจากค่าจดหมายนี้
2. จากนั้นเริ่มหมุนการคำนวณของคุณเช่นยุ่งเหยิงของด้าย ถ้าขอบของก้อนหนึ่งเป็น "a" ให้อีกอันหนึ่งเป็น "a" ด้วย ถัดไปคุณจะต้องคำนวณพื้นที่ของใบหน้าและใบหน้าเป็นสี่เหลี่ยมเดียวกันตามปกติ - สี่เหลี่ยมสี่เหลี่ยมที่รู้จักกันทั้งหมด². ก้อนในแนวทแยงยังไม่ยากที่จะวัดด้วยใช้ทฤษฎีบทพีทาโกรัสซึ่งเท่ากับ "a" คูณด้วยรากที่สองของทั้งสอง จำไว้ว่าประมาณพูดก้อนนี้เป็นตารางปริมาตร, การคำนวณหนึ่งที่คุณจะได้รับเกือบทุกอย่าง
3. ตอนนี้เราสามารถดำเนินการคำนวณอื่น ๆ ได้ตัวอย่างเช่นพื้นที่ของลูกบาศก์ซึ่งตามที่เราได้กล่าวไว้ข้างต้นแล้วคือ 6a². นั่นคือรู้พื้นที่ของใบหน้า - เราจะหาพื้นที่และก้อนทั้งหมด เกือบจะเหมือนกันเราสามารถหาปริมาตรของลูกบาศก์ได้ จากข้อเท็จจริงที่ว่าปริมาตรมีค่าเท่ากับ a³แล้วทุกด้านจะเท่ากับค่าของ "a" ซึ่งหมายความว่าไม่สามารถหาก้อนได้อย่างง่ายดาย

ดังนั้นในวิธีง่ายๆคุณได้เรียนรู้ว่าคุณต้องการดำเนินการอะไรในการคำนวณลูกบาศก์ใด ๆ ทดลองทดลอง!