สมบัติของรูปสามเหลี่ยมมุมเขียว

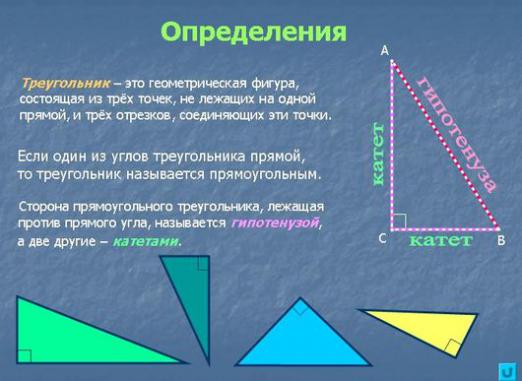
รูปสี่เหลี่ยมผืนผ้าเป็นรูปทรงเรขาคณิตที่มุมหนึ่งเป็นเส้นตรง รูปสามเหลี่ยมที่มีมุมฉากมีคุณสมบัติเป็นจำนวนมาก
คุณสมบัติพื้นฐาน
ดังนั้นสมบัติของรูปสามเหลี่ยมมุมฉากมีดังนี้:
สิ่งแรกและที่สำคัญที่สุดคือมุมขวาด้วยซึ่งเขาได้รับชื่อ เท่าที่ทราบก็เท่ากับ 90 องศา อีกสองมุมในจำนวนรวมควรมีค่านี้ ดังนั้นในภาพผลรวมของทุกมุมควรเป็น 180 องศา - นี่คือสมบัติของมุมของรูปสามเหลี่ยมมุมฉากที่ด้านขวา
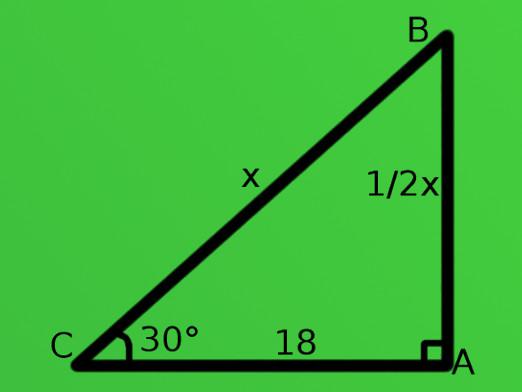
ประการที่สองทรัพย์สินสำคัญคือคู่สัญญารูปสามเหลี่ยมสี่เหลี่ยมผืนผ้า: ด้านตรงข้ามและสองขา cathetus ของรูปสามเหลี่ยมมุมปากซึ่งอยู่ตรงข้ามมุม 30 องศาเท่ากับครึ่งหนึ่งของด้านตรงข้าม
ทฤษฎีบทพีทาโกรัส
สมบัติของรูปสามเหลี่ยมขนมขุนมากอัน ได้แก่ ทฤษฎีบทพีทาโกรัส: สี่เหลี่ยมจัตุรัสของด้านตรงข้ามจะเท่ากับพลังของสี่เหลี่ยมจัตุรัสของขา
C2 = a2 + b2, a และ b คือขาและ c คือด้านตรงข้าม
พื้นที่ของรูปสามเหลี่ยมขนมขนัดขวามีค่าเท่ากับครึ่งหนึ่งของขา: S = 1 / 2ab
คุณสมบัติของ Median
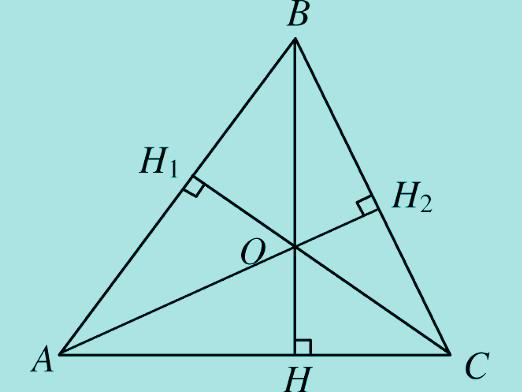
นอกจากนี้ควรสังเกตและคุณสมบัติของค่ามัธยฐานในรูปสามเหลี่ยมมุมฉากด้านขวา ค่ามัธยฐานที่อยู่ตรงข้ามกับครึ่งหนึ่ง
ถ้าเราวาดความสูงจากจุดยอดในรูปสามเหลี่ยมมุมเขียวซึ่งเท่ากับ 90เกี่ยวกับ ไปทางด้านตรงข้ามแล้วรูปสามเหลี่ยมจะถูกแบ่งออกเป็นสองส่วนรูปสามเหลี่ยมรูปสี่เหลี่ยมเดียวกัน จากนี้เราสามารถสรุปได้ว่าความสูงในรูปสี่เหลี่ยมผืนผ้าเป็นรูปสามเหลี่ยมทางเรขาคณิตของทั้งสองส่วนของด้านตรงข้าม ดังนั้นแต่ละ cathet จะมีสัดส่วนโดยเฉลี่ยกับส่วนที่อยู่ถัดจากด้านข้าง นอกจากนี้คุณจำเป็นต้องรู้ด้วยว่าความสูงที่ลดลงไปทางด้านตรงข้ามกับด้านข้างจะสัมพันธ์กับขาในอัตราส่วน: 1 / a2 + 1 / b2 = 1 / f2 , ที่ a และ b เป็นขาและ f คือความสูง