วิธีการหาเส้นทแยงมุมของรูปทรงสี่เหลี่ยมคางหมู?
ก่อนที่คุณจะทราบวิธีหาเส้นทแยงมุมtrapezium จำสิ่งที่เป็นรูปสี่เหลี่ยมคางหมู ในรูปทรงสี่เหลี่ยมคางหมู, รูปสี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมขนมเปียกปูนที่มีสองด้านตรงกันข้ามขนานกัน ด้านขนานเหล่านี้เรียกว่าฐานของรูปสี่เหลี่ยมคางหมูและส่วนอื่น ๆ เรียกว่าด้านข้าง ด้านข้างสามารถเหมือนกันได้แล้วเราจะจัดการกับรูปสี่เหลี่ยมคางหมูหน้าจั่ว
ในสิ่งต่อไปนี้ให้เราตรวจสอบรายละเอียดลำดับการค้นหาความยาวเส้นทแยงมุมสำหรับกรณีทั่วไปของ trapezium ไม่ใช่หน้าจั่ว เราจะดำเนินการต่อจากข้อเท็จจริงที่ว่าข้อมูลเริ่มต้นคือความยาวของทั้งสี่ด้านของรูปสี่เหลี่ยมคางหมูมุมที่ฐานไม่เป็นที่รู้จัก
การคำนวณเส้นทแยงมุม trapezium

ใน ABCD รูปสี่เหลี่ยมคางหมูแสดงในรูปมีสอง diagonals AC และ BD ลำดับของการค้นหาความยาวของพวกเขาก็เหมือนกันดังนั้นให้พิจารณาทุกอย่างเกี่ยวกับตัวอย่างของการค้นหา BD ทแยงมุมตรงข้ามกับ˂BAD
BD ทแยงมุมพร้อมกันด้านข้างของรูปสามเหลี่ยม ABD และสามารถคำนวณโดยโคไซน์ทฤษฎีบทโดยใช้สูตร:
BD = √ (AB2+ โฆษณา2-2AB.AD.cos ˂ BAD)
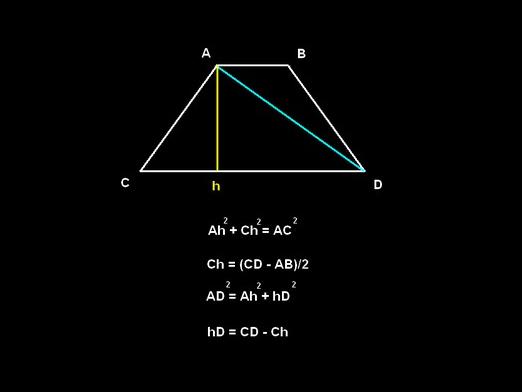
ในสูตรนี้เราทราบปริมาณทั้งหมดยกเว้นโคไซน์˂ BAD ในการคำนวณเราจำเป็นต้องทำการแปลงภาพขนาดเล็ก "ตัดออก" รูปสี่เหลี่ยมผืนผ้า BNMC จากรูปสี่เหลี่ยมคางหมูเดิม เป็นผลให้เราได้รูปสามเหลี่ยม ABD "ซึ่งด้าน BD" เท่ากับด้านข้างของแผ่นสี่เหลี่ยมคางหมู

˂BAD "ในรูปสามเหลี่ยมคือ˂BADในรูปสี่เหลี่ยมคางหมูดังนั้นเนื่องจากเราไม่ได้ทำการเปลี่ยนแปลงใด ๆ กับรูปสามเหลี่ยม ABN ดังนั้นใน ABD รูปสามเหลี่ยมนี้ "ด้าน AB เป็นที่รู้จักกับเราด้าน BD" = CD และด้าน AD "= AD - NM = AD - BC
ปรากฎว่าด้วยทฤษฎีบทโคไซน์ cos ˂BAD = cos ˂BAD "= (AB2 + AD "2 - BD "2) / 2AB.AD "= (AB2 + (AD-BC)2 - CD2) / 2AB.(AD - BC)
การเปลี่ยนนิพจน์นี้เป็นสูตรที่พบก่อนหน้านี้เราได้รับ:
BD = √ (AB2+ โฆษณา2-2AB.AD.cos ˂BAD) = √ (AB2+ โฆษณา2-2AB.AD.(AB2 + (AD-BC)2 - CD2) / 2AB.(AD - BC)) = √ (AB2 + โฆษณา2 - AD.(AB2 + (AD-BC)2 - CD2) / (AD - BC)) = √ (AB2 + โฆษณา2 - AD.(AD - BC)2/ (AD - BC) - AD.(AB2 - CD2) / (AD - BC)) = √ (AB2 + โฆษณา2 - AD2 + โฆษณา.ปีก่อนคริสตกาล - ค.ศ..(AB2 - CD2) / (AD - BC)) = √ (AB2 + โฆษณา.ปีก่อนคริสตกาล - ค.ศ..(AB2 - CD2) / (AD-BC))
BD = √ (AB2 + โฆษณา.ปีก่อนคริสตกาล - ค.ศ..(AB2 - CD2) / (AD-BC))
สูตรที่ได้รับสำหรับเส้นทแยงมุมของรูปสี่เหลี่ยมคางหมูสามารถใช้ได้กับค่าความยาวของด้านข้างของจัตุรัสเดิม
สำหรับเส้นทแยงมุมที่สองสูตรจะมีรูปแบบดังนี้:
AC = √ (ซีดี2 + โฆษณา.ปีก่อนคริสตกาล - ค.ศ..(CD2 - AB2) / (AD-BC))
เส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูน
หากคุณสนใจในการหาเส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนทรงกระบอกจะทำให้สูตรที่ได้ง่ายขึ้นอย่างมาก หลังจากทั้งหมดในรูปสี่เหลี่ยมคางหมู AB = CD, AB ดังนั้น2 - CD2 = 0 และสูตรสำหรับความยาวของเส้นทแยงมุมจะลดลงในรูปแบบ:
BD = √ (AB2 + โฆษณา.BC)
เส้นทแยงมุมของรูปสี่เหลี่ยมคางหมูเป็นหน้าจั่วเท่ากับกันดังนั้นเส้นทแยงมุมที่สองจะถูกพบตามสูตรเดียวกัน
ในกรณีที่มีข้อมูลเริ่มต้นความยาวของฐาน trapezium ด้านใดด้านหนึ่งและมุมที่ฐานจากนั้นปัญหาในการหาเส้นทแยงมุมของ trapezoid ลดลงในการคำนวณด้านข้างของรูปสามเหลี่ยมโดยทฤษฎีบทโคไซน์









